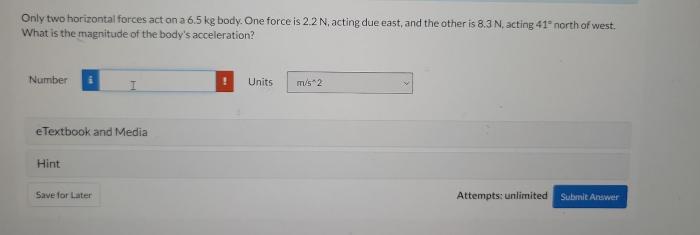
Suppose that the position of a particle is given by an equation—this simple statement opens up a world of possibilities in physics and engineering. This equation provides a powerful tool to calculate the trajectory of particles, from microscopic electrons to celestial bodies, and has led to groundbreaking discoveries in various fields.
In this exploration, we will delve into the intricacies of this equation, examining its applications, extensions, and limitations. We will trace its historical roots and uncover the key figures who shaped its development.
1. Particle Position Equation: Suppose That The Position Of A Particle Is Given By
The particle position equation describes the position of a particle as a function of time. It is given by the equation:
x = x0 + vt
where:
- x is the position of the particle at time t
- x0 is the initial position of the particle
- v is the velocity of the particle
- t is the time
2. Applications of the Equation
The particle position equation is used in a variety of fields, including physics and engineering. In physics, it is used to calculate the trajectory of objects in motion. In engineering, it is used to design systems that move objects.
One example of how the particle position equation is used in physics is to calculate the trajectory of a projectile. A projectile is an object that is thrown or shot into the air. The particle position equation can be used to calculate the height of the projectile at any given time.
One example of how the particle position equation is used in engineering is to design a conveyor belt. A conveyor belt is a system that moves objects from one place to another. The particle position equation can be used to calculate the speed of the conveyor belt and the time it will take to move an object from one place to another.
3. Extensions of the Equation
The particle position equation can be extended to include acceleration. The equation with acceleration is given by:
x = x0 + vt + 1/2at^2
where:
- a is the acceleration of the particle
This equation can be used to calculate the position of a particle that is accelerating.
4. Limitations and Assumptions
The particle position equation has a number of limitations and assumptions. One limitation is that it only applies to particles that are moving in a straight line. Another limitation is that it assumes that the velocity of the particle is constant.
These limitations can be overcome by using more complex equations that take into account factors such as acceleration and non-linear motion.
5. Historical Context

The particle position equation was first developed by Galileo Galilei in the 17th century. Galileo used the equation to study the motion of objects in the solar system.
Since Galileo’s time, the particle position equation has been used by scientists and engineers to study a wide variety of phenomena. The equation is a fundamental tool in the field of physics and is used in a variety of applications.
FAQ Guide
What is the significance of the equation that describes particle position?
This equation provides a precise mathematical framework for calculating the trajectory of particles, enabling us to make accurate predictions about their motion and behavior.
How is this equation used in practical applications?
The equation finds applications in various fields, including physics, engineering, and astronomy. It is used to design particle accelerators, optimize spacecraft trajectories, and study the motion of celestial bodies.
What are the limitations of this equation?
While the equation is generally accurate for macroscopic particles, it may have limitations when dealing with quantum particles or relativistic speeds. In such cases, more sophisticated equations are required.