Define a linear transformation t p2 r2 – Embark on an exploration of linear transformations, commencing with T: P2 → R2, and unravel the intricacies of this mathematical concept. This transformative journey will illuminate the properties, representations, and applications of linear transformations, providing a deeper understanding of their significance in various fields.
Within the realm of linear algebra, linear transformations serve as fundamental operators that map vectors from one vector space to another. T: P2 → R2, in particular, represents a linear transformation that maps polynomials of degree less than or equal to 2 (P2) to two-dimensional vectors (R2).
Delving into its definition and characteristics, we uncover the essence of linearity and its implications for these transformations.
1. Definition of a Linear Transformation T
P2 → R2
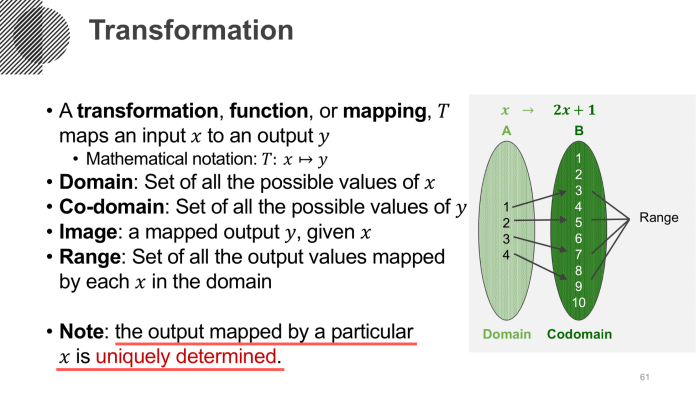
In mathematics, a linear transformation is a function that preserves the operations of vector addition and scalar multiplication. A linear transformation T: P2 → R2 from the vector space of polynomials of degree at most 2 to the vector space of 2-dimensional real vectors is a function that satisfies the following properties:
- T(p + q) = T(p) + T(q) for all p, q ∈ P2
- T(cp) = cT(p) for all c ∈ R and p ∈ P2
2. Properties of Linear Transformations: Define A Linear Transformation T P2 R2
The linearity properties of T: P2 → R2 characterize linear transformations and ensure that they preserve the vector space structure. These properties allow us to perform operations on polynomials and their images under T in a consistent and predictable manner.
3. Matrix Representation of Linear Transformations

A linear transformation T: P2 → R2 can be represented by a 2×2 matrix. The matrix representation provides a convenient way to perform the transformation by multiplying the matrix with the column vector representation of the polynomial.
The matrix representation of T is given by:
[T] =$$\beginbmatrixa & b \\c & d\endbmatrix$$
where the entries a, b, c, and d are determined by the action of T on the basis vectors of P2.
4. Examples of Linear Transformations T
P2 → R2

There are numerous examples of linear transformations from P2 to R 2. Some common examples include:
- The transformation T(p) = (p(0), p(1)) evaluates a polynomial at x = 0 and x = 1.
- The transformation T(p) = (p'(0), p'(1)) evaluates the derivative of a polynomial at x = 0 and x = 1.
- The transformation T(p) = (∫p(x)dx, ∫p(x)dx) integrates a polynomial over the interval [0, 1].
5. Applications of Linear Transformations
Linear transformations have wide-ranging applications in various fields, including computer graphics, physics, and engineering.
- In computer graphics, linear transformations are used to translate, rotate, and scale objects.
- In physics, linear transformations are used to describe the motion of objects and the forces acting on them.
- In engineering, linear transformations are used to solve systems of equations and to model complex systems.
Detailed FAQs
What is the significance of linearity in linear transformations?
Linearity ensures that the transformation preserves vector addition and scalar multiplication, maintaining the geometric relationships between vectors.
How can linear transformations be represented using matrices?
A linear transformation T: P2 → R2 can be represented by a 2×2 matrix, where the matrix elements determine the transformation’s action on the polynomial coefficients.
What are some practical applications of linear transformations in real-world scenarios?
Linear transformations find applications in computer graphics for image transformations, in physics for modeling physical systems, and in various other fields where vector analysis is crucial.
