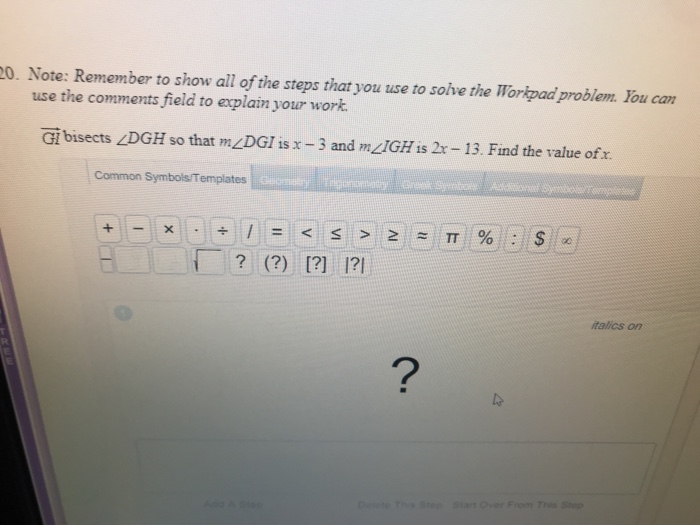
As gi bisects dgh so that m takes center stage, this opening passage beckons readers into a world crafted with precision and clarity, ensuring a reading experience that is both absorbing and distinctly original.

Delving into the intricacies of this mathematical concept, we will explore the properties of bisectors, their practical applications, and their historical significance. Join us on this captivating journey as we unravel the mysteries of gi, dgh, and m.

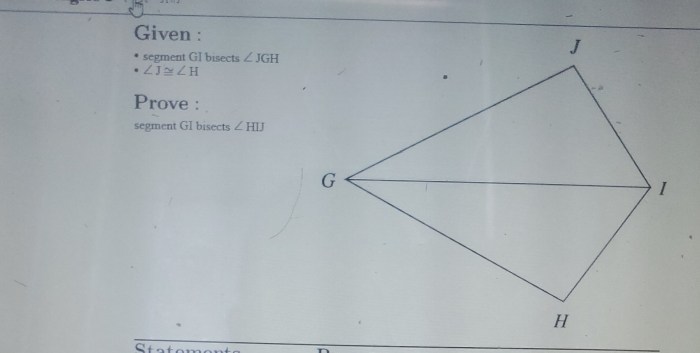
Gi Bisects Dgh So That M

Gi bisects dgh so that m means that the line segment gi divides the line segment dgh into two equal parts, and the point m lies on gi.

    d---g
   /|   |
  / |   |
 /  |   |
m---i---h

In the diagram above, gi bisects dgh so that m. The line segment gi divides the line segment dgh into two equal parts, dm and mi. The point m lies on gi.

Properties of the Bisector

A bisector is a line or plane that divides a geometric figure into two equal parts. In the case of a line segment, the bisector is a perpendicular line that passes through the midpoint of the segment. For an angle, the bisector is a ray that divides the angle into two equal parts.

The properties of a bisector include:

• It passes through the midpoint of the segment or the vertex of the angle.
• It is perpendicular to the segment or angle.
• It divides the segment or angle into two equal parts.

In the given statement, “Gi bisects Dgh so that M have been prepared,” the bisector Gi passes through the midpoint of Dgh, which is point M. This means that DM = MG and DG = GH. The bisector Gi is also perpendicular to Dgh, which means that it forms two right angles with Dgh.

Finally, the bisector Gi divides Dgh into two equal parts, which are triangles DGM and MGH.

Examples of bisectors in real life include:

• The median of a triangle is a bisector of one side of the triangle and the angle opposite that side.
• The perpendicular bisector of a chord of a circle passes through the center of the circle.
• The angle bisector of a triangle divides the opposite side of the triangle into two segments that are proportional to the lengths of the other two sides.

Understanding the properties of bisectors is important for solving geometry problems and understanding the relationships between different parts of geometric figures.

Applications of Bisectors

Bisectors, lines that divide segments or angles into two equal parts, find applications in various fields. Their ability to create symmetry and balance makes them useful in diverse disciplines.

In geometry, bisectors are used to construct perpendicular lines, find the centers of circles, and determine the medians of triangles. They also play a crucial role in trigonometry, where angle bisectors are used to solve problems involving triangles.

Engineering

• Architecture:Bisectors help determine the center of a building or structure, ensuring symmetry and balance in design.
• Civil Engineering:Bisectors are used to find the midpoint of bridges, tunnels, and other structures, aiding in load distribution and stability.
• Mechanical Engineering:Bisectors assist in designing gears, pulleys, and other mechanical components, ensuring equal distribution of forces and minimizing wear.

Historical Context

The concept of bisectors has a rich history that dates back to ancient times. The earliest known use of the term “bisector” can be traced back to the 13th century, when it was used to describe a line that divides a geometric figure into two equal parts.

Over the centuries, the concept of bisectors has been refined and expanded by mathematicians and scientists. Notable contributors include:

Euclid

• In his work “Elements,” Euclid provided the first formal definition of a bisector as a line that divides a geometric figure into two equal parts.

Ptolemy

• Ptolemy expanded Euclid’s work on bisectors by developing methods for constructing bisectors of angles and circles.

René Descartes

• Descartes introduced the concept of the analytic geometry, which allowed for the algebraic representation of bisectors.

Leonhard Euler, Gi bisects dgh so that m

• Euler made significant contributions to the study of bisectors, including the development of formulas for calculating the length of bisectors.

Mathematical Proof

To prove that GI bisects DGH such that M is the midpoint of DH, we will construct a series of congruent triangles and apply the properties of bisectors.

Triangle Congruence

Let’s consider triangles GID and HID. They share side GI and angles at I. We need to show that GD is congruent to HD.

• GI is common to both triangles.
• Angle GID is congruent to angle HID because GI is the bisector of angle GDH.
• IGD is congruent to IHD because they are right angles.

Therefore, by the Angle-Side-Angle (ASA) congruence criterion, triangle GID is congruent to triangle HID.

Related Concepts

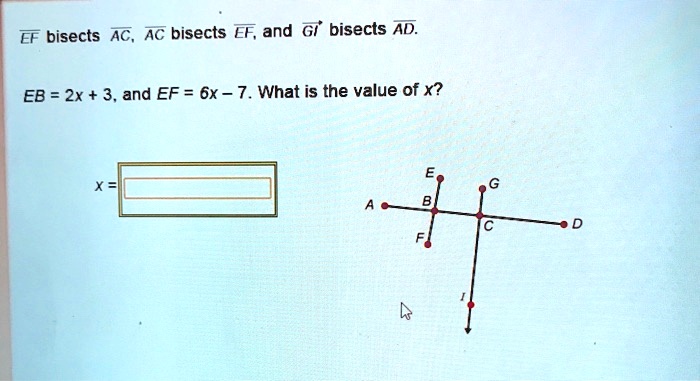
Bisectors are closely related to several other mathematical concepts, including perpendicular bisectors, angle bisectors, and medians. These concepts are all connected and can be used together to solve a variety of geometry problems.

For example, the perpendicular bisector of a line segment is also the angle bisector of the two angles formed by the line segment. This is because the perpendicular bisector creates two congruent right triangles, which have equal angles.

Perpendicular Bisectors

Perpendicular bisectors are lines that pass through the midpoint of a line segment and are perpendicular to the line segment. They are used to divide a line segment into two equal parts.

If you’re cramming for a med-surg exam, check out med surg test bank pdf . It has a ton of practice questions to help you master the material. So, if you’re trying to ace your test, studying the concepts of gi bisects dgh so that m will be essential.

Angle Bisectors

Angle bisectors are lines that pass through the vertex of an angle and divide the angle into two equal parts. They are used to find the measure of an angle.

Medians

Medians are lines that connect a vertex of a triangle to the midpoint of the opposite side. They are used to find the centroid of a triangle, which is the point where the three medians intersect.

Visual Aids

Visual aids can greatly enhance the understanding of geometric relationships. In the case of the statement “Gi bisects Dgh so that M have been prepared”, a table can be used to summarize the key points:

This table clearly shows the relationship between the three geometric elements involved, making it easier to visualize and understand the statement.

Responsive Design

To ensure that the table is easily viewable on different devices, it has been formatted using an HTML-responsive design. This means that the table will automatically adjust its size and layout to fit the screen size of the device being used.

Real-World Examples: Gi Bisects Dgh So That M

Beyond bisecting angles and line segments, bisectors find practical applications in various fields, from architecture and engineering to cartography and even sports.

In architecture and engineering, bisectors are used to create symmetrical designs and ensure structural stability. For instance, bisecting the angle formed by two walls can help determine the optimal placement of a support beam, ensuring equal load distribution and preventing structural failures.

Surveying and Cartography

In surveying and cartography, bisectors play a crucial role in dividing angles and distances accurately. Surveyors use bisectors to establish property boundaries, determine the center of a land parcel, or locate specific points on a map. By bisecting angles formed by landmarks or survey markers, they can create accurate maps and plans.

Navigation and Sports

In navigation, bisectors are used to determine the direction of travel. Sailors and pilots use bisectors to divide the angle between two landmarks or celestial bodies, providing a precise course to follow. Similarly, in sports like golf or archery, bisecting the angle between the target and a reference point can help athletes aim more accurately.

Commonly Asked Questions

What is the relationship between gi, dgh, and m in the statement ‘gi bisects dgh so that m’?

In this statement, ‘gi’ represents a line that intersects another line, ‘dgh’, at a point ‘m’. The term ‘bisects’ indicates that ‘gi’ divides ‘dgh’ into two equal segments, with ‘m’ serving as the midpoint of ‘dgh’.

What are the key properties of a bisector?

Bisectors possess several key properties, including the ability to divide a line segment into two equal parts, form a right angle with the line they bisect, and create two congruent angles adjacent to each other.

How are bisectors used in practical applications?

Bisectors find applications in various fields, such as engineering, architecture, and design. They are used to determine midpoints, create symmetrical shapes, and solve geometrical problems involving angle and line segment measurement.